Recently, one new quasi-unit-cell of quasicrystals was discovered experimentally by Zhanbing He's groupin State Key Laboratory for Advanced Metals and Materials, University of Science and Technology Beijing, with the collaboration with Prof. Chuang Dong of Dalian Jiaotong University and Prof.Walter Steurer of ETH Zurich, Switzerland.
Quasiperiodic structures can be described geometrically either as decorated tilings or as coverings. While quasiperiodic tilings are based on two or more unit-tiles, coverings can cover the plane (space) by partially overlapping copies of a single structural repeat-unit (quasi-unit-cell). Such a quasi-unit-cell, when decorated with atoms (atomic cluster), is the counterpart to a unit cell of a periodic structure. It allows a more physical description of a quasicrystal structure than the structurally fully-equivalent tiling-based models do. In the case of decagonal quasicrystals, the so-far most frequently used quasi-unit-cell is based on the Gummelt decagon; if the quasi-unit cell approach is employed at all.
Importantly, Prof. He's group in University of Science and Technology Beijing reported a novel kind of experimentally identified quasi-unit-cell for quasicrystals. It is a fundamental decagonal unit with a diameter of approximately 2 nm, and consists of four subunits: three flattened hexagons and one bow-tie (D3H+1BT,for short, the kind of Lück decagon). Compared with the previous quasi-unit cell of Gummelt's decagon with strict matching rules, the new quasi-unit-cell of Lück decagon has advantages of combining tiling and covering, which is more flexible and without strict matching rules. Therefore it is suitable for more general cases of quasicrystals, especially for most observed imperfect quasicrystals. The finding of this Lück-decagon based quasi-unit-cell shows that quasiperiodic order in real decagonal quasicrystals is possible based on a variety of fundamental structural subunits (quasi-unit cells). Both, the Gummelt as well as the Lück covering have in common that their actual 3D structural subunits are arranged along quasi-lattice planes with traces forming Fibonacci pentagrids. These planes may be important for the evolution of quasiperiodic long-range order.
For details, please see: Haikun Ma, Zhanbing He*, Hua Li, Tiantian Zhang, Shuang Zhang, Chuang Dong, Walter Steurer, Novel kind of decagonal ordering in Al74Cr15Fe11.Nat. Commun.11,6209(2020). https://doi.org/10.1038/s41467-020-20077-4
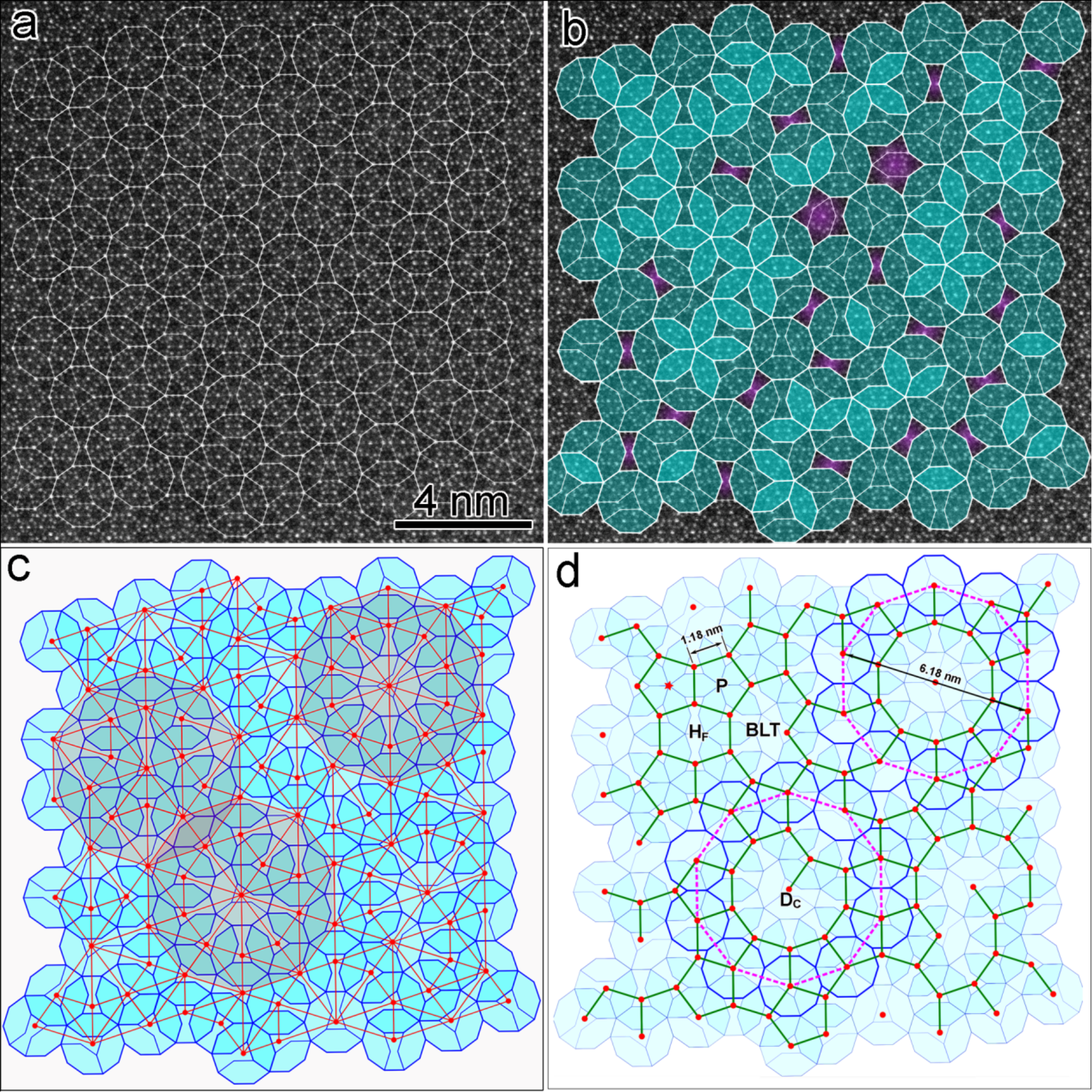
Covering based on the Lück decagon.a, HAADF-STEM image along the tenfold axis of decagonal Al74Cr15Fe11 with a Lück-decagon covering superposed. b, The Lück decagons are shaded blue to clearly show some defective areas marked in purple. c, If the centers of the Lück decagons (red dots) are connected by lines a triangle tiling is created, which resembles the Tübingen triangle tiling (TTT). d, Creation of a tiling by linking the centers of overlapping Lück decagons in c.